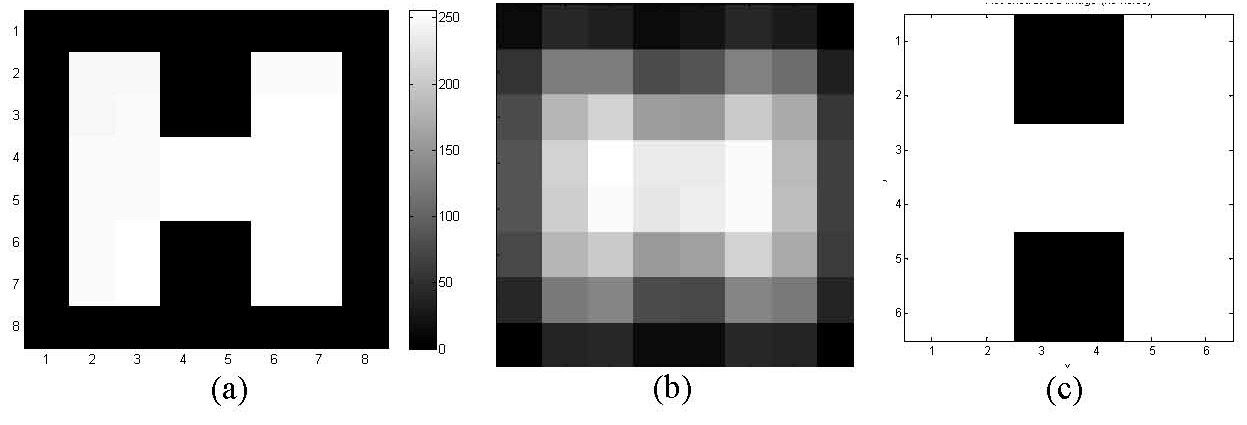
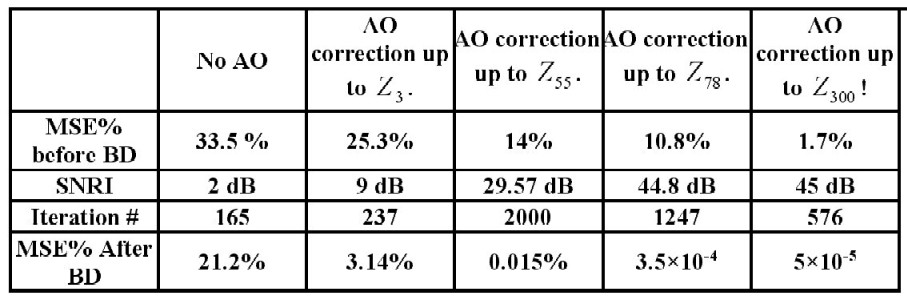
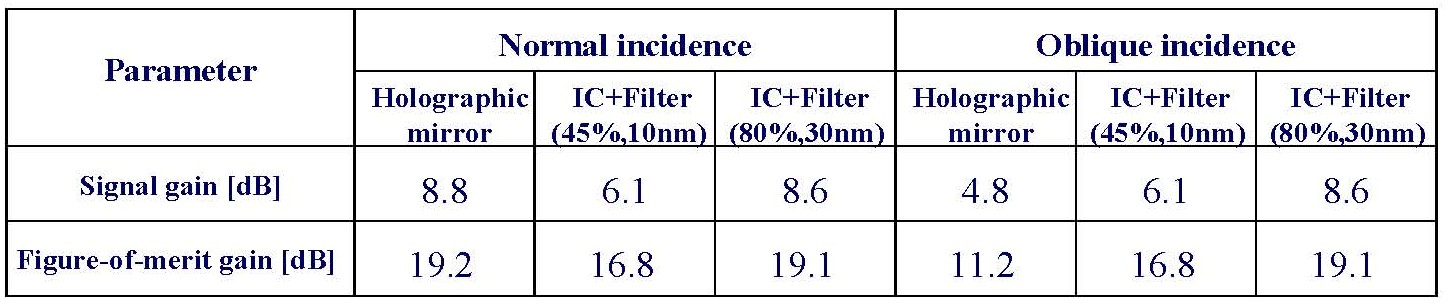
Heterogeneous Networks

Future  Heterogeneous Communications Networks

____________________________________________________________________________________________________

MIMO Free Space Optical Communications using Multiple Light Beams Propagation through Atmospheric Turbulence

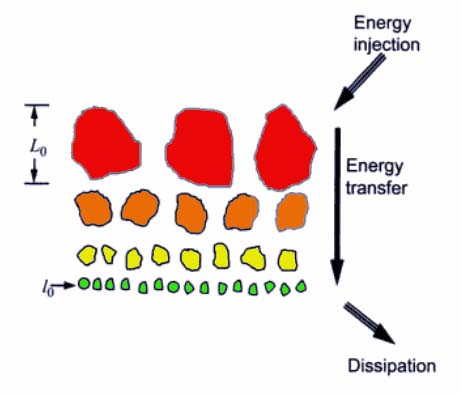
 Free space optical communication (FSOC) is a promising technology for high bandwidth wireless communication links over a long distance where a fiber or wire is unfeasible or where RF communication is inadequate. The link performance of FSOC can be severely degraded by atmospheric turbulence induced effects including intensity fluctuations, phase fluctuations, beam wandering and beam jittering. Atmospheric turbulence strength would become stronger with increasing Rytov variance related to the refractive index structure parameter Cn2 and the propagation distance L. Under the strong turbulence regime, scintillation index increases beyond unity, reaches its maximum value in the focusing regime and decreases toward unity in the saturation regimes. Recent experiments have shown significant deviations from the Kolmogorov model in some layers of the atmosphere, which has prompted research on optical wave propagation through non-Kolmogorov atmospheric turbulence.

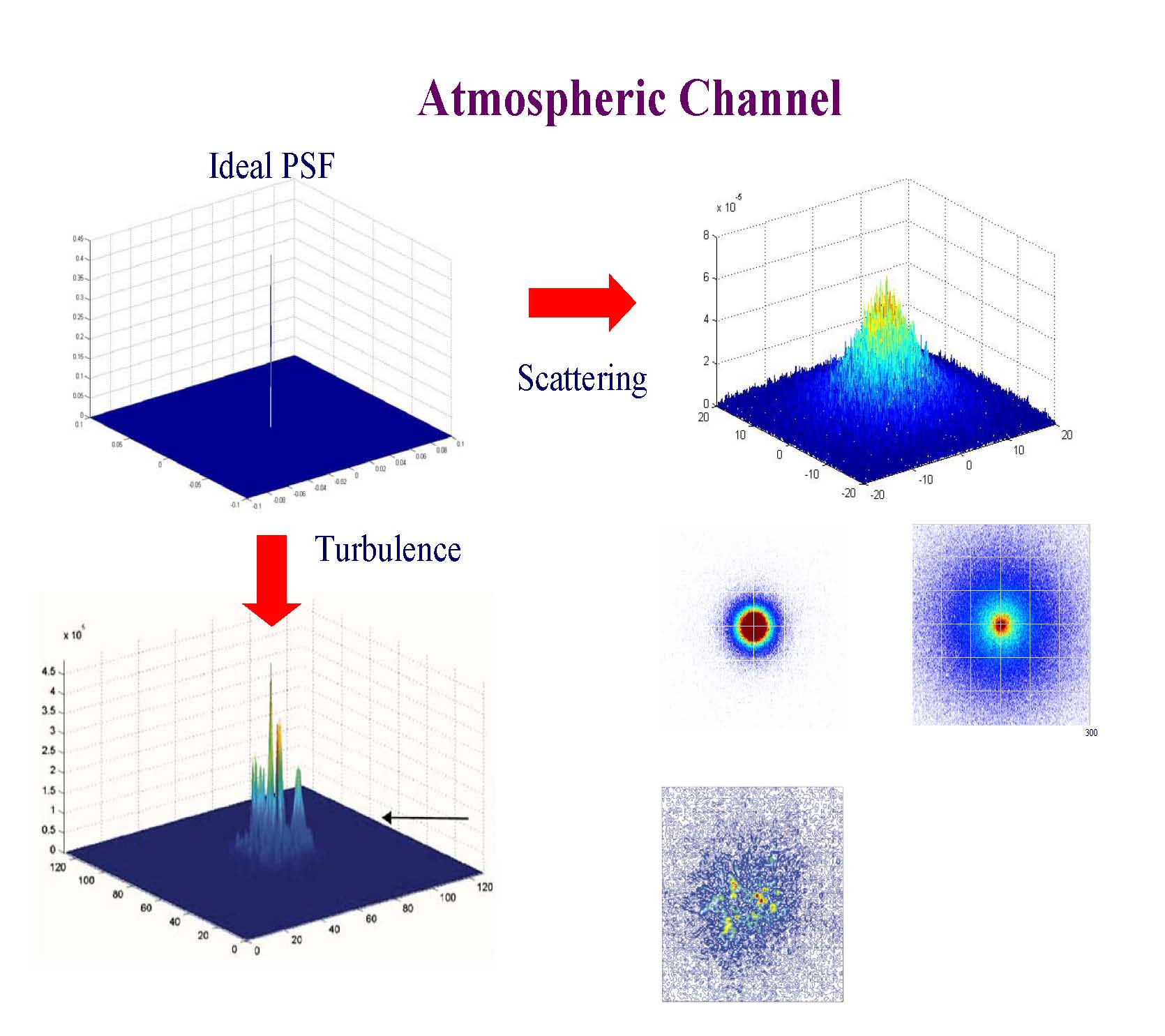
 The intensity fluctuations or scintillation at the receiver reduces FSOC channel capacity. In order to improve system performance, scintillation can be mitigated by means of reducing the spatial coherence of the transmitted beam and the spatial diversity using multiple transmitted beams and multiple receivers.

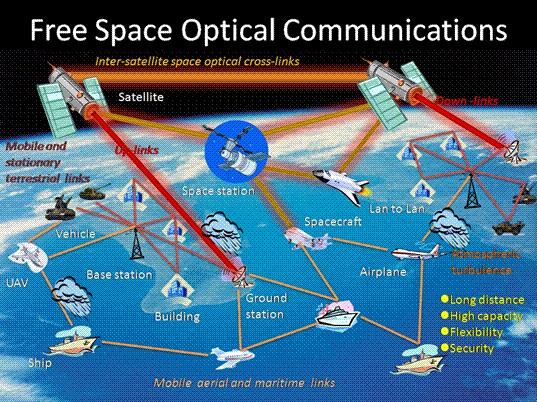
Fig.-1. Free Space Optical Communications

Partially coherent beams with reduced spatial coherence show lower scintillation at the cost of larger divergence angle and lower average received power. Partially coherent beams have a lower scintillation than fully coherent beams. However, a partially coherent beam has a larger beam spreading and forms a large spot in the receiver aperture, which leads to a loss of the transmitted energy being received by the detector. By optimizing the spatial coherence length, the improvement in scintillation reduction can overcome the penalty of power reduction and significant signal-to-noise ratio gains can be obtained in weak atmospheric turbulence.

Spatial diversity using multiple transmitted beams and multiple receivers can also be employed to reduce scintillation and ultimately improve FSO channel capacity. It has been shown that the scintillation of a beam array can be reduced by carefully adjusting the spatial separation of beamlets. However, scintillation of a beam array will increase significantly if the spatial separation of beamlets is smaller than the correlated length. In addition, the received energy from the beam arrays is low unless the constituent beamlets are inclined to overlap at the receiver aperture, which is difficult to achieve over long propagation distances. The use of multiple transmitters and receivers has also been suggested for use in multiple-input–multiple-output (MIMO) configurations.

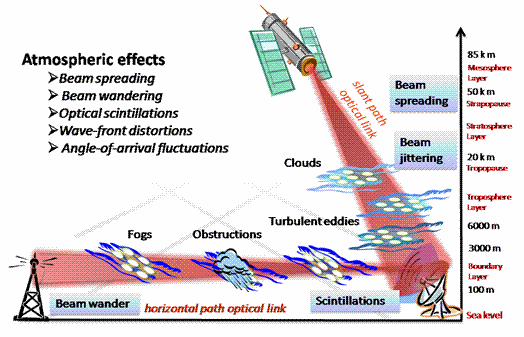
Fig.-2. Atmospheric effects on Free Space optical communications

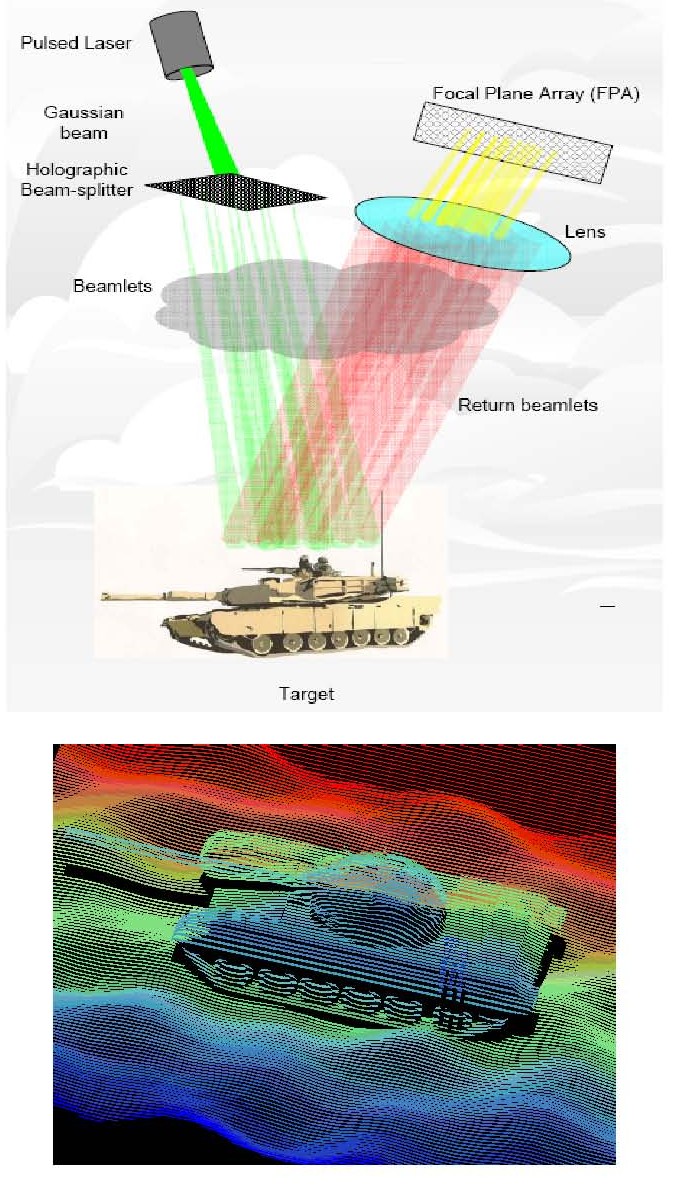
Typically FSOC receiver employs the acquisition, tracking and pointing (ATP) mechanism to point the receiver’s narrow field of view (FOV) at the small divergence transmitted beam. This approach is impractical for many mobile applications requiring small size and low weight, so a wide FOV optical receiver is needed to eliminate the large, gimbals based mechanism. As shown in Fig 3(a), a wide FOV receiver can be achieved by using a single-element fisheye lens group to collect the wide field beam, and a steering mirror to couple the beam into a multi-mode fiber.

Professor Joseph Kahn of Stanford University and Mr. Djahani, in an overview paper entitled; “Imaging Diversity Receivers for high-Speed Infrared Wireless Communication,” [2] describes these contributions as:

 

·         Implementation of multi-branch angle diversity using non-imaging elements requires a separate optical concentrator for each receiving element, which may be excessively bulk and costly. Yun and Kavehrad proposed the fly-eye receiver [1], which consists of a single imaging optical concentrator (e.g., a lens) that forms an image of the received light on a collection of photo-detectors, thereby separating signals that arrive from different directions. In this article, we refer to this design as an imaging angle-diversity receiver, or simply an imaging receiver. Implementation of an angle-diversity receiver using imaging optics offers two advantages over a non-imaging implementation. First, all photo-detectors share a common concentrator, reducing size and cost. Second, all the photo-detectors can be laid out in a single planar array, facilitating the use of a large number of receiving elements or pixels.

 

·         In non-Line-of-Sight (LoS) wireless optical links, Yun and Kavehrad [1] also proposed the spot-diffusing transmitter, which utilizes multiple narrow beams pointed in different directions, as a replacement for the conventional diffuse transmitter, which utilizes a single broad beam aimed at an extended reflecting surface. In this article, we refer to the spot-diffusing transmitter as a multi-beam or quasi-diffuse transmitter. While the diffuse transmitter provides considerable immunity against beam blockage near the receiver, it yields a high path loss. The quasi-diffuse transmitter is expected to reduce path loss compared to the diffuse transmitter, because the narrow beams experience little path loss traveling from the transmitter to the illuminated reflective surfaces.

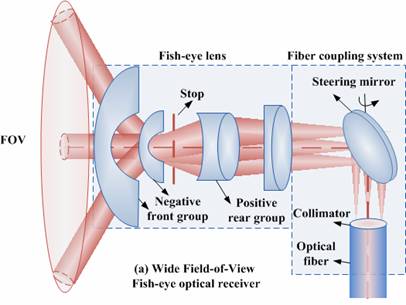
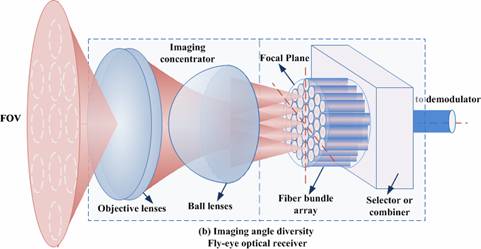
Fig.-3. Wide field-of-view diversity optical receivers for free space optical communications

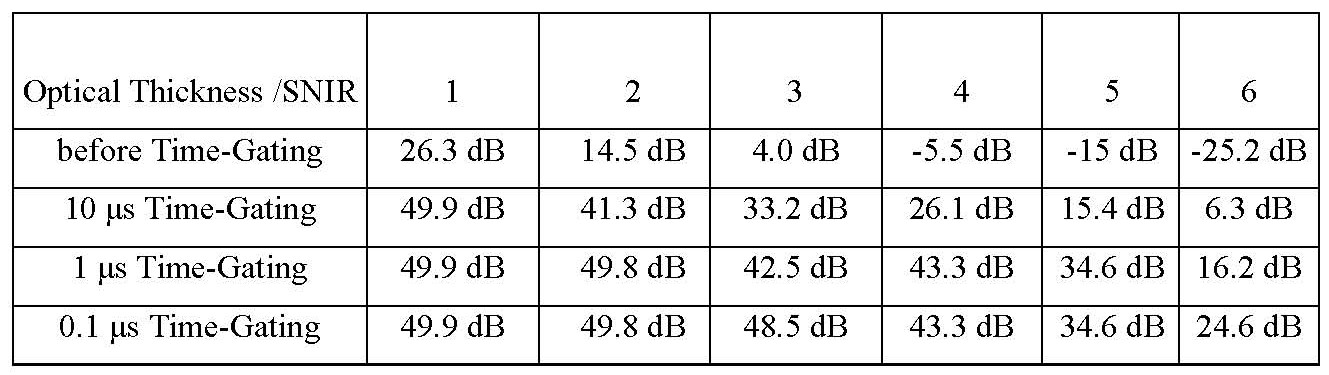
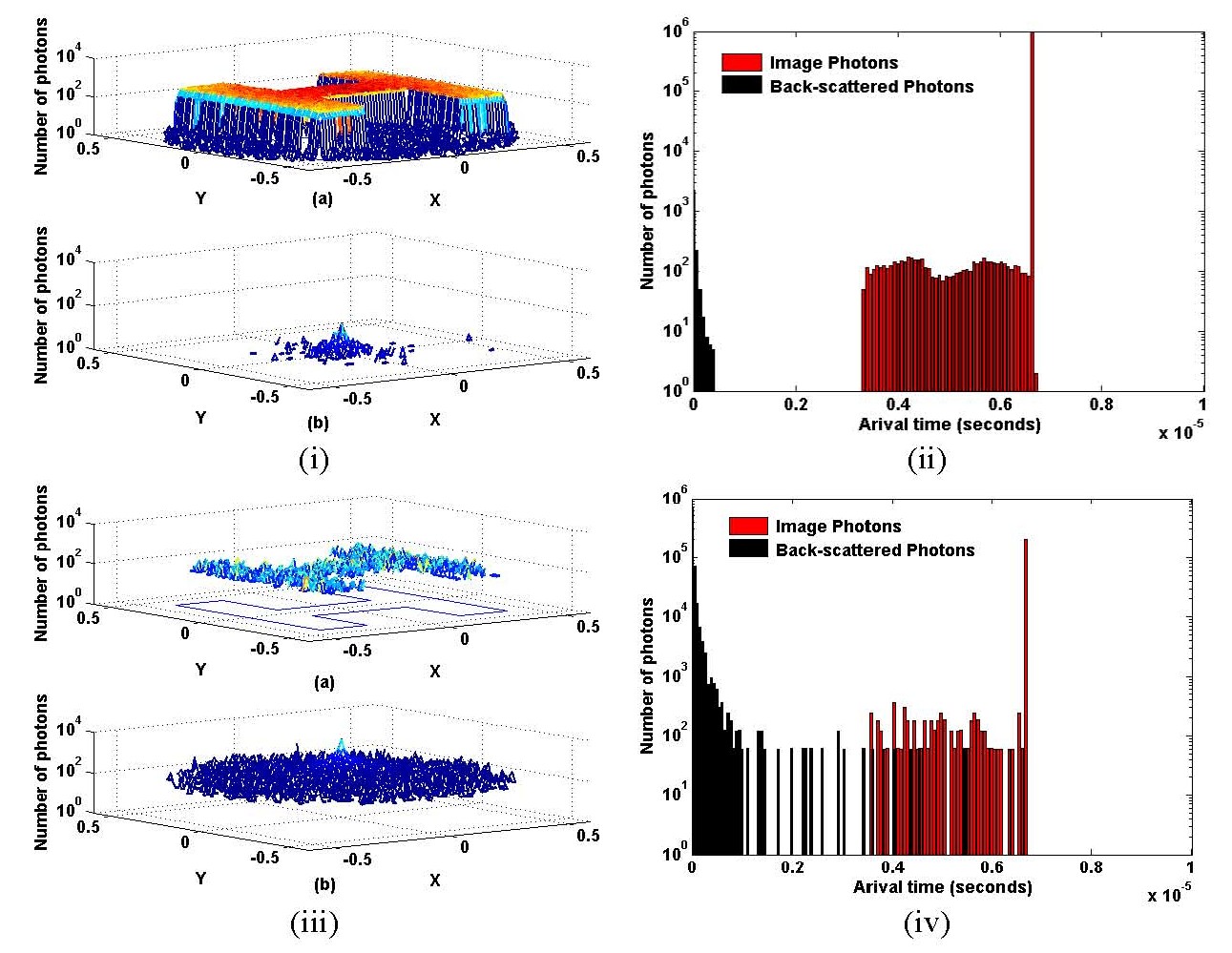
Compared with the single input single output FSOC system, we investigate BER performance of wide FOV diversity optical receiver of Multiple Input Multiple Output (MIMO) FSOC for laser beam propagation through moderate-strong atmospheric turbulence. Figure 4(a) shows BER performance of various MIMO FSOC systems as a function of SNR after 1000 m propagation through strong turbulence. The results demonstrate a significant decrease in BER as the number of diversity transmitters/receivers is increased. The results shown in Figure 4(b) for BER as a function of distance reveals the BER approaches to the maximum at distance of 1500 m and diversity receivers reduce the BER performance over long distance, as diversity apertures average out the scintillations of multi-beams with decreasing coherent length in strong turbulence. For more details, see references [3] through [5].

Fig. 4(a) BER versus SNR for SISO and MIMO FSOC, (b) BER vs transmission distance for SISO and MIMO FSOC

 

1.      1.  G. Yun, M. Kavehrad, "Spot-Diffusing and Fly-Eye Receivers for Indoor Infrared Radio Communications," IEEE Int. Conf. on Selected Topics in Wireless Communications, Vancouver, June 1992.

2.      Joseph Kahn, et al., “Imaging Diversity Receivers for high-Speed Infrared Wireless Communication,” IEEE Communications Magazine, Vol. 36, No. 12, pp. 88-94, December 1998.

3.      P. Deng, M. Kavehrad, Z. Liu, Z. Zhou, and X. Yuan, "Capacity of MIMO Free Space Optical communications using multiple partially coherent beams propagation through non-Kolmogorov strong turbulence," Opt. Express 21(13), 15213-15229, 2013.

4.      P. Deng, X. Yuan, M. Kavehrad, M. Zhao and Y. Zeng, "Off-axis catadioptric fisheye wide field-of-view optical receiver for free space optical communications," Optical Engineering 51(6), 063002, 2012.

5.      P. Deng, M. Kavehrad and X. Yuan, "Comparing Wide Field-of-View Optical Receivers for Free Space Optical Communications," in The IEEE Photonics Society 2012 Summer Topical Meetings, Seattle, 2012.

____________________________________________________________________________________________________

 

 

Propagation of Radial Airy Array Beams through Atmospheric Turbulence

 

The array beams, constructed by combining multiple separate beamlets, have attracted much attention due to their wide applications to technical areas such as high-power laser systems, free-space optical communications, active optical imaging systems, etc. Up to now, the propagation properties of various types of array beams, such as the linear, rectangular and radial ones, in free space or in atmospheric turbulence have been investigated in detail. Meanwhile, many special beam types with various transverse intensity profiles, e.g., the elliptical Gaussian, Hermite-Gaussian, circular dark hollow and flat-topped beams, were considered as the beamlets of the array beams.

 

 

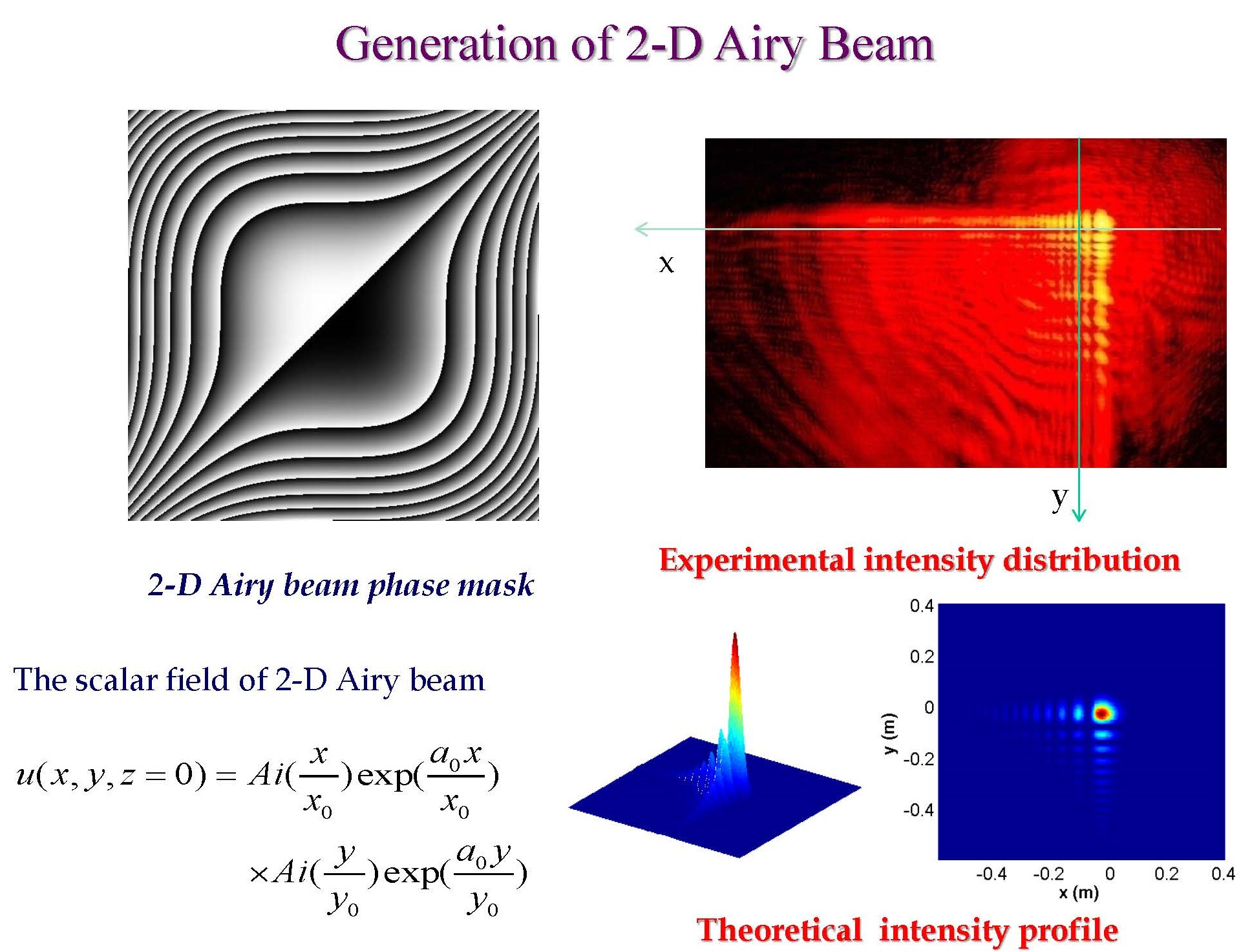
 Recently, several authors have addressed the propagation properties of Airy beams in atmospheric turbulence, showing that the Airy beams are more resilient against turbulence-induced perturbations than the conventional Gaussian ones. This fact implies that Airy beams have the potential for offering some advantages if they are used in applications involving beam propagation in atmospheric turbulence. Hence, it is interesting to develop an array beam by combining multiple Airy beamlets. The average intensity distribution of an Airy array beam is an important quantity in practice. To deeply understand the average-intensity-distribution evolution of Airy array beams passing through atmospheric turbulence, the theoretical formulations of their average intensity are desirable.

 

 In practice, two types of beamlet combination are usually considered. One is the phase-locked combination, and the other is the non-phase-locked combination. In this project, we first formulated the average intensity of both phase-locked and non-phase-locked radial Airy array beams propagating in atmospheric turbulence, and then examined the average-intensity-distribution evolution of these array beams in atmospheric turbulence in sufficient details.

 

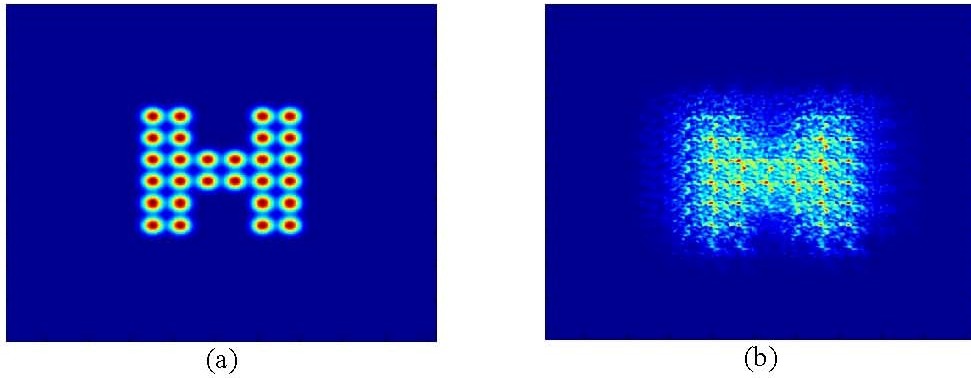
We have considered that a radial Airy array beam, which consists of N equal off-axis Airy beamlets situated uniformly on a ring as shown by an example of N = 4 in Fig. 1, propagates along the positive z-axis in atmospheric turbulence.

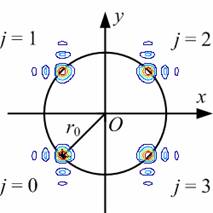
Fig. 1. Schematic illustration of a radial Airy array beam constructed by four equal off-axis beamlets.

The evolution of the normalized average intensity along the 45º axis in the x-y plane of a single Airy beam during propagation in both free space and atmospheric turbulence is illustrated by Fig. 2. 

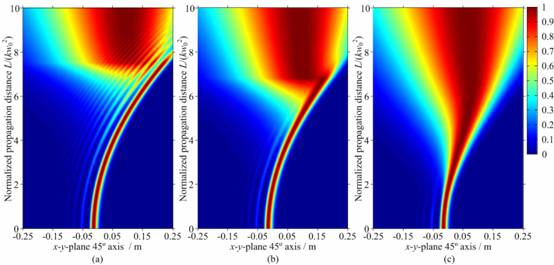
Fig. 2. The evolution of the normalized average intensity along the 45º axis in the x-y plane of a single Airy beam during propagation in both free space and atmospheric turbulence, where the normalization is obtained by scaling the average intensity at a certain propagation distance by its highest value at that propagation distance. λ = 1550 nm. (a) Cn2 = 0; (b) Cn2 = 10−15 m−2/3; (c) Cn2 = 10−14 m−2/3.

The transverse average intensity patterns of phase-locked Airy array beams propagating in both free space and atmospheric turbulence are shown by Fig. 3.

Fig. 3. Transverse average intensity patterns of phase-locked Airy array beams propagating in both free space and atmospheric turbulence, where λ = 1550 nm, N = 4 and tx = ty = 66 mm. (a) L = 1 km, Cn2 = 0; (b) L = 3 km, Cn2 = 0; (c) L = 8 km, Cn2 = 0; (d) L = 1 km, Cn2 = 10−14 m−2/3; (e) L = 3 km, Cn2 = 10−14 m−2/3; (f) L = 8 km, Cn2 = 10−14 m−2/3.

The transverse average intensity patterns of non-phase-locked Airy array beams propagating in both free space and atmospheric turbulence are shown by Fig. 4.

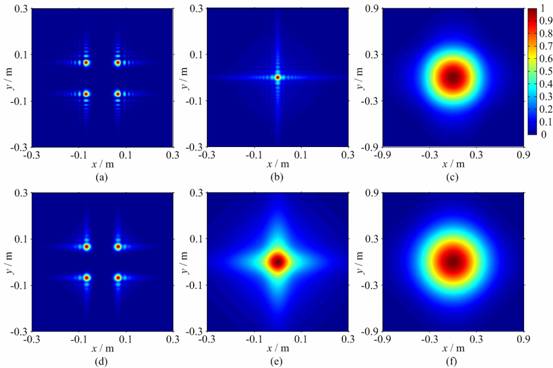
Fig. 4. Transverse average intensity patterns of non-phase-locked Airy array beams propagating in both free space and atmospheric turbulence, where λ = 1550 nm, N = 4 and tx = ty = 66 mm. (a) L = 1 km, Cn2 = 0; (b) L = 3 km, Cn2 = 0; (c) L = 8 km, Cn2 = 0; (d) L = 1 km, Cn2 = 10−14 m−2/3; (e) L = 3 km, Cn2 = 10−14 m−2/3; (f) L = 8 km, Cn2 = 10−14 m−2/3.

The longitudinal cross-section average intensity distributions of phase-locked Airy array beams with varying Airy-beamlet parameters are illustrated by Fig. 5.

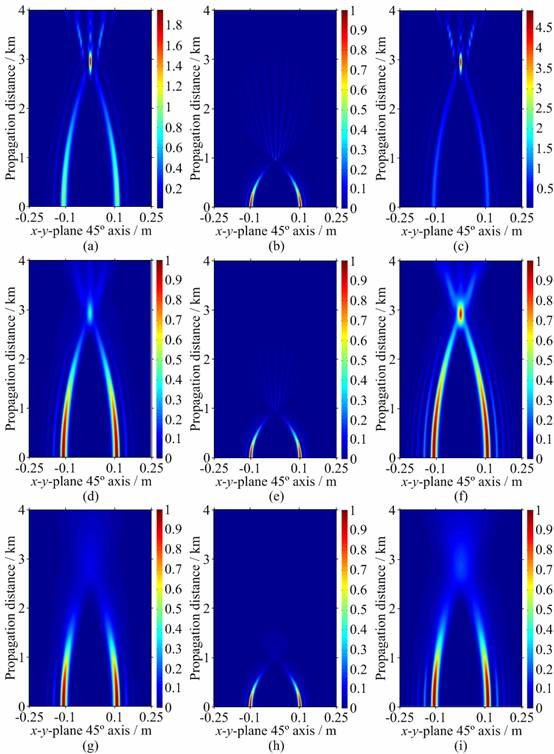
Fig. 5. Longitudinal cross-section average intensity distributions of phase-locked Airy array beams with varying Airy-beamlet parameters, where λ = 1550 nm, N = 4, tx = ty = 66 mm. (a) Cn2 = 0, w0 = 12 mm, a = 0.1; (b) Cn2 = 0, w0 = 6 mm, a = 0.1; (c) Cn2 = 0, w0 = 12 mm, a = 0.05; (d) Cn2 = 10−15 m−2/3, w0 = 12 mm, a = 0.1; (e) Cn2 = 10−15 m−2/3, w0 = 6 mm, a = 0.1; (f) Cn2 = 10−15 m−2/3, w0 = 12 mm, a = 0.05; (g) Cn2 = 10−14 m−2/3, w0 = 12 mm, a = 0.1; (h) Cn2 = 10−14 m−2/3, w0 = 6 mm, a = 0.1; (i) Cn2 = 10−14 m−2/3, w0 = 12 mm, a = 0.05.

The longitudinal cross-section average intensity distributions of non-phase-locked Airy array beams with varying Airy-beamlet parameters are shown by Fig. 6.

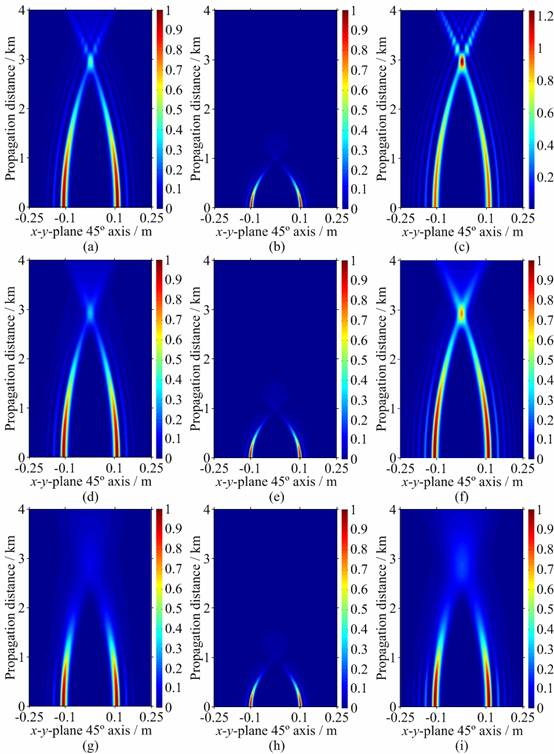
Fig. 6. Longitudinal cross-section average intensity distributions of non-phase-locked Airy array beams with varying Airy-beamlet parameters, where λ = 1550 nm, N = 4, tx = ty = 66 mm. (a) Cn2 = 0, w0 = 12 mm, a = 0.1; (b) Cn2 = 0, w0 = 6 mm, a = 0.1; (c) Cn2 = 0, w0 = 12 mm, a = 0.05; (d) Cn2 = 10−15 m−2/3, w0 = 12 mm, a = 0.1; (e) Cn2 = 10−15 m−2/3, w0 = 6 mm, a = 0.1; (f) Cn2 = 10−15 m−2/3, w0 = 12 mm, a = 0.05; (g) Cn2 = 10−14 m−2/3, w0 = 12 mm, a = 0.1; (h) Cn2 = 10−14 m−2/3, w0 = 6 mm, a = 0.1; (i) Cn2 = 10−14 m−2/3, w0 = 12 mm, a = 0.05.

__________________________________________________________________________________________________ 

Network-Enabled RF/Optical Wireless Communications

 

- Wavelet Packet Transmission Systems

As proven by the success of OFDM, multi-carrier modulation has been recognized as an efficient solution for wireless communications. Waveform bases other than sine functions could similarly be used for multi-carrier systems in order to provide an alternative to OFDM. For example, wavelet packet modulation (WPM) for transmission over wireless channels, is shown to be overall quite similar to OFDM, but with some interesting additional features and improved characteristics.

Though the principle of multi-carrier modulation is not recent, its actual use in commercial systems had been delayed until the technology required to implement it became available at reasonable costs. Similarly, the idea of using more advanced transform than Fourier’s as the core of a multi-carrier system has been introduced more than a decade ago. However, such alternative methods have not been viewed with major interest and therefore have received little attention. With the current demand for high performance in wireless communication systems, one is entitled to wonder about the possible improvement that wavelet-based modulation could exhibit compared to OFDM systems.

Several objectives motivate the current research on WPM. First, the characteristics of a multi-carrier modulated signal are directly dependent on the set of waveforms of which it makes use. Hence, the sensitivity to multi-path channel distortion, synchronization error or non-linear amplifiers might present better values than a corresponding OFDM signal. Little attention has been given to the evaluation of those system level characteristics in the case of WPM. Moreover, the major advantage of WPM is its flexibility. This feature makes it eminently suitable for future generation of communication systems. With the ever-increasing need for enhanced performance, communication systems can no longer be designed for average performance while assuming channel conditions. Instead, new generation systems have to be designed to dynamically take advantage of the instantaneous propagation conditions. This situation has led to the study of flexible and reconfigurable systems capable of optimizing performance according to the current channel response. A tremendous amount of work has been done recently to fulfill this requirement at the physical layer of communication systems: complex equalization schemes, dynamic bit-loading and power control that can be used to dynamically improve system performance. While WPM can take advantage of all those advanced functionalities designed for multi-carrier systems, it benefits also from an inherent flexibility. This feature together with a modular implementation complexity makes WPM potential candidate for building highly flexible modulation schemes. Wavelet theory has been foreseen by many investigators as a good platform on which to build multi-carrier waveform bases.

 

- Network-Enabled RF/Free Space Optical (FSO) Communications

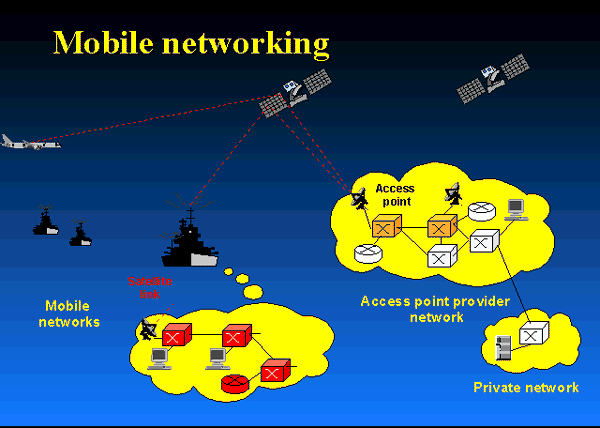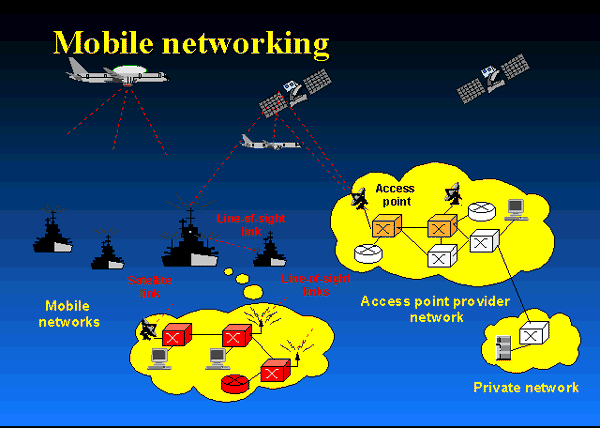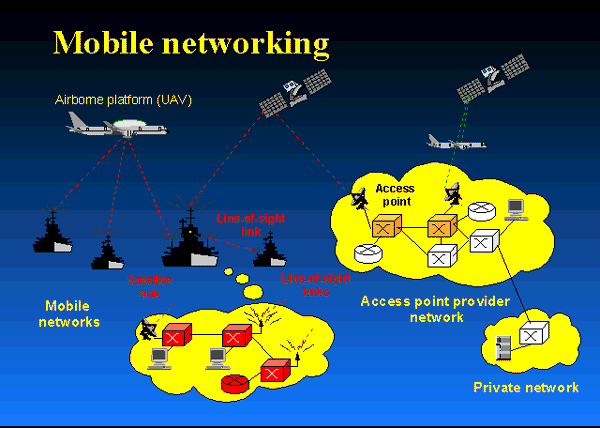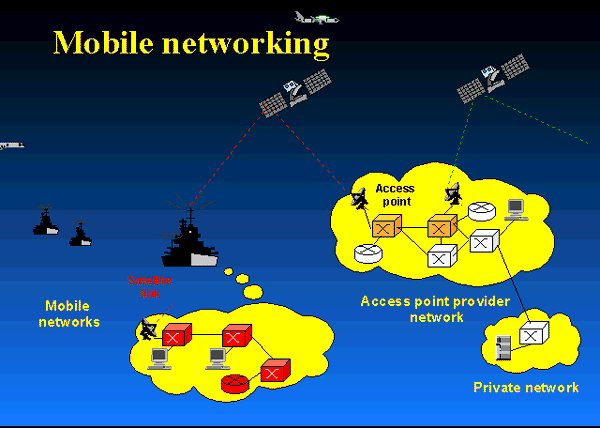
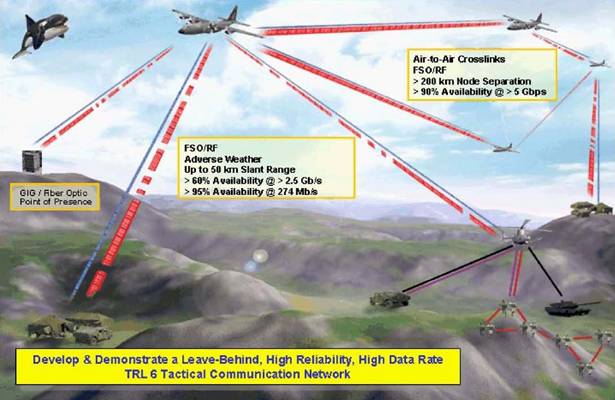
Needless to say, where line-of-sight is available (see the figure below), using ultra-short laser pulses, one may achieve the ultimate wideband over unregulated optical frequency bands, using Free-Space-Optical (FSO) or a hybrid of RF/FSO links. Then one is able to beam optical band to distant points. This approach could help bring optical bandwidth, capable of carrying huge amounts of information, to applications ranging from wireless communications between air and ground vehicles on the battlefield, to short links between college campus buildings or to metropolitan area networks that connect all the buildings in a city.

 

The papers below are based on a recently devised new methodology (Patent) to pack the data into rapid-fire bursts of light that can blast through fog and clouds. This new system uses ultra-short pulses of laser light that provide greater bandwidth and improved reliability over conventional optical wireless links. The approach uses a technique called "Fractal Modulation", which is a form of Wavelet Packet Modulation (WPM), to produce wavelets that can co-exist in a signal channel without interference, and provide frequency and time diversity, concurrently. By sending the same message at several different rates (multi-rate), one can get through adverse weather conditions.

Using Fractal modulation, each receiver has a menu to choose the best received signal transmission rate, thus adaptation is feed-forward. At the same time, wavelets have the desirable properties of being both time and frequency limited, thus are able to pack a large amount of power in very short pulses, in addition to providing inherent diversity:

 

    • A 100 fs pulse at 100 mJ would produce a peak power of 1 Terawatt. At 2 Giga pulse per second, this is 200 Mega Watts of average power. With today’s nano-second technology, a Terawatt of peak power would require laser energies of 1000 J.

 

Ultra-short Pulse Shaping Experimental Set-up

(CICTR LABS)

 

 

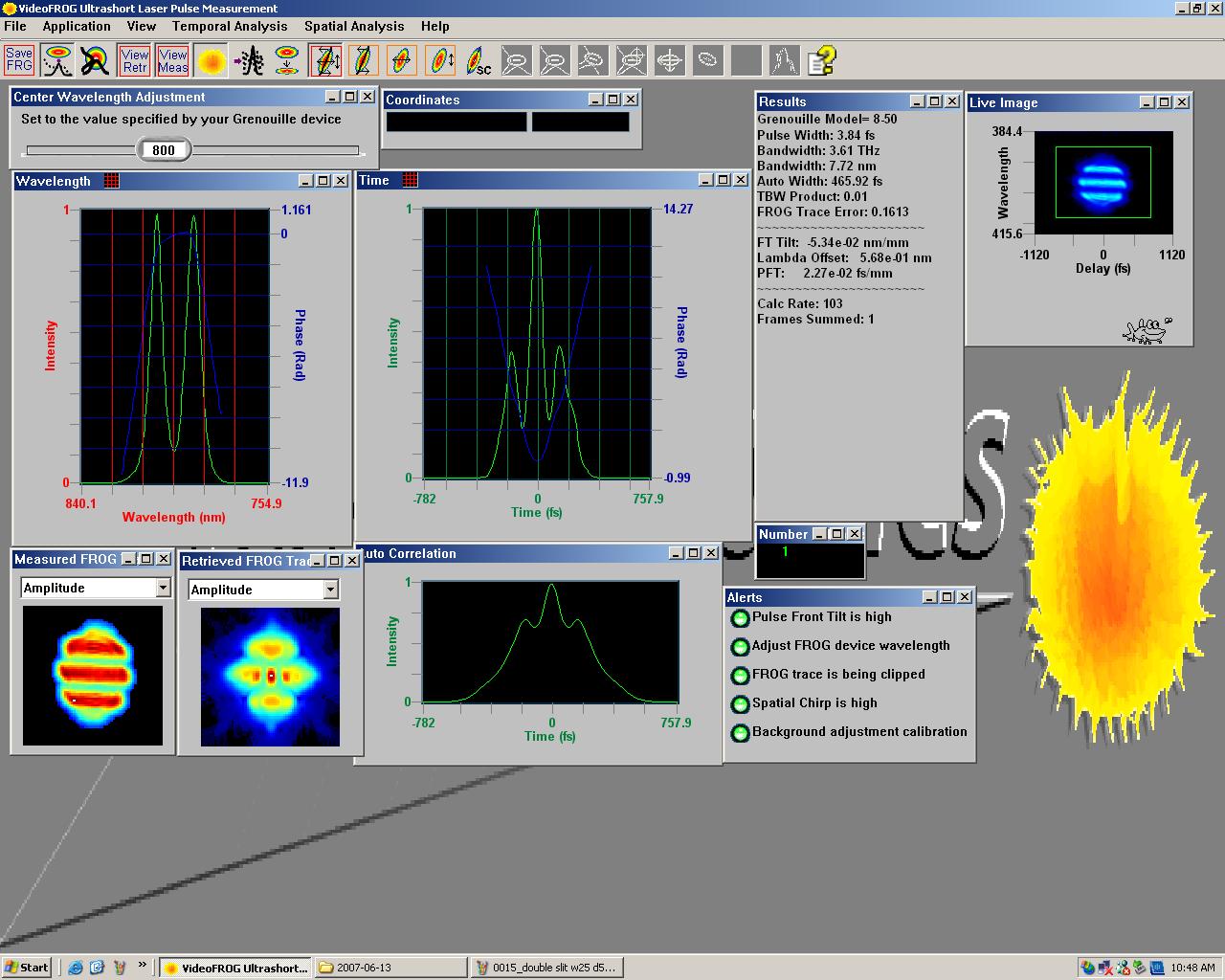
Real-Time 460 Femto-second Meyer Wavelet Shaped Pulse at a 3 Giga Pulse per Second Rate

(Intensity Correlation Image at CICTR LABS)

Spatial and temporal matched filtering can then be applied through Spectral Encoding and Decoding of frequency components of the broadband ultra-short light pulses. The encoding/decoding may be realized all-optically through photolithographic masks or other types of spatial light modulators.

The space-time focusing properties of this approach can lead to a new class of wireless “Opportunistic Communications” systems with significant advantages over current RF approaches. Using this approach, one is liberated from the many constraints of spectrum allocation and regulation. The spatial focusing potential of this approach is an appealing quality, in power saving and would allow accommodating as many users as possible within it. Interference issues of shared RF bands are non-existent here.

Potential applications include commercial wireless as well as specialized systems, such as secure communication systems that demand a low probability of intercept.

See also; DARPA ORCLE.

  • S. Lee and M. Kavehrad,”Airborne Laser Communications with Impulse Response Shortening and Viterbi  Decoding,” Proceedings of the IEEE MILCOM, Washington, D.C., October 2006.

 

Acknowledgments

A DARPA Grant sponsored by the U.S. Air Force Research Laboratory/Wright-Patterson AFB Contract-FA8650-04-C-7114 and The Pennsylvania State University CICTR has supported this research.

___________________________________________________________________________

 

Active MIMO Laser Imaging through Cloudy and Turbulent Atmosphere

    Imaging of distant target objects is important for military and airborne surveillance. Reconnaissance missions require proper imaging capability to correctly identify targets and reduce the probability of false alarm. Imaging by means of photography is a passive way of obtaining target information, which is supplemented by Radar imaging. However, light wavelengths are preferable due to higher resolution and visual interpretation comfort. This leads to active laser imaging which is comparable to flash photography. In clear weather and visibility conditions, active imaging can be conducted in both day and night times. However, under cloudy and turbulent weather and battlefield conditions, resolution and contrast greatly diminishes in traditional imaging. Cloud and fog contribute to Mie scattering of light, resulting in attenuation and backscatter interference, whereas turbulence causes blurring of images, i.e. loss of resolution.

Kolmogorov Cascade Theory of Turbulence

Outer scale ( L 0) and inner scale ( l 0 ) set the sizes of eddies that form the inertial region

 

Cloud Formation

Turbulent air creates small-scale fluctuations of the refractive index along a waveform propagation path - causing random amplitude, phase and angle-of-arrival variations known as Turbulence.

Turbulence distorts an optical beam cross-section spatially, causing random beam dancing, phase-front distortion, etc,  in imaging. These spatial adverse effects contribute to image blurring.

In transmissions or communications using simple Intensity Modulation / Direct Detection, turbulence lends itself approximately to a multiplicative Lognormal fading coefficient (flat fading) - known as scintillation which is a temporal effect.

Where there is moisture, turbulent air can create an upward motion of moist air particles and this is a prerequisite in formation of clouds. Once a cloud is formed,  light beam photons traveling through along a propagation path are scattered due to Mie scattering. Received optical power loss associated with light beam passing through clouds, for the most part, is a loss to scattering rather than absorption.

These problems can be ameliorated by equipping imaging apparatuses with novel signal processing techniques.

    Inspired by Yun & Kavehrad’s [1]; multi-beam quasi-diffuse transmitter and fly-eye imaging receiver indoor wireless optical communications link, a spatially multiplexed MIMO imaging system is proposed and the corresponding performance and image quality is analyzed in a turbid and turbulent atmosphere.

Multi-Beam Quasi-Diffuse Transmitter and Fly-Eye Imaging Receiver

    We originated and designed concepts for a Multi-Input-Multi-Output (MIMO) wireless optical architecture referred to as Multi-Spot Diffuse (MSD) configuration with Multi-element optical transmitters and multi-branch optical receivers, proposed in [1].

Professor Joseph Kahn of Stanford University and Mr. Djahani, in an overview paper entitled; “Imaging Diversity Receivers for high-Speed Infrared Wireless Communication,”[2] describes these contributions as:

  •    Implementation of multi-branch angle diversity using non-imaging elements requires a separate optical concentrator for each receiving element, which may be excessively bulk and costly. Yun and Kavehrad proposed the fly-eye receiver [1], which consists of a single imaging optical concentrator (e.g., a lens) that forms an image of the received light on a collection of photo-detectors, thereby separating signals that arrive from different directions. In this article, we refer to this design as an imaging angle-diversity receiver, or simply an imaging receiver. Implementation of an angle-diversity receiver using imaging optics offers two advantages over a non-imaging implementation. First, all photo-detectors share a common concentrator, reducing size and cost. Second, all the photo-detectors can be laid out in a single planar array, facilitating the use of a large number of receiving elements or pixels.

  •      In non-Line-of-Sight (LoS) wireless optical links, Yun and Kavehrad [1] also proposed the spot-diffusing transmitter, which utilizes multiple narrow beams pointed in different directions, as a replacement for the conventional diffuse transmitter, which utilizes a single broad beam aimed at an extended reflecting surface. In this article, we refer to the spot-diffusing transmitter as a multi-beam or quasi-diffuse transmitter. While the diffuse transmitter provides considerable immunity against beam blockage near the receiver, it yields a high path loss. The quasi-diffuse transmitter is expected to reduce path loss compared to the diffuse transmitter, because the narrow beams experience little path loss traveling from the transmitter to the illuminated reflective surfaces.

    The following publications [3-11] establish the superiority of a MIMO active imaging system, based on the fly-eye receiver for optical communications, in harsh conditions. A high-power laser beam is split into several beamlets, representing pixels, which illuminate a wide area, thereby increasing search rate. The spacing between beamlets, which is a parameter controlling interference among the beamlets and blurring, may be adapted depending on visibility conditions.

Active Optical Imaging Lidar

The parameters that can be adapted are:

 

·        Spacing of the beamlets

·        Number of the beamlets

·        Power in each beamlet

By varying these quantities, a soft trade-off for better quality in imaging can be achieved. For example, in thicker clouds, less number of beamlets with higher power in each would yield better results; on the other hand, in high turbulence clear weather (no clouds), wider spacing among beamlets would give us the best results.

The quality-determining factor in active imaging is the SNR per pixel, which can be improved by time-gating and post-processing. Figure 1 shows results from Monte-Carlo Imaging through clouds of optical thickness of 1 (2 round-trip) and 4 (8 round-trip) respectively. It is obvious that time-gating removes unwanted backscatter interference, and improves SNR, i.e. contrast.

The resulting SNR improvements are summarized in Table 1.

Figure-1.  Spatial (i, iii) and temporal (ii, iv) distributions of Image and backscatter photons in clouds of optical thickness 1 (2 roundtrip) (i, ii) and 4 (8 roundtrip) (iii, iv).

Table 1. Contrast Improvement using time-gates of different lengths.

Turbulence imposes a different type of challenge, manifested in the loss of resolution. This is illustrated by Figure 2, which shows the point spread function or PSF under moderate turbulence conditions.

Figure 2.  Point Spread Function under moderate turbulence condition.


    To combat this phenomenon, we propose the use of holographic beam-splitters to divide the laser beam into several beamlets (Figure 3), and use imaging receivers to obtain target images (the letter ‘H’ in this case in Figures 4 and 5).

Figure 3. (a) Holographic Beam-splitter, (b) Output beamlets froma 4x4 beam-splitter.

 

Figure 4. Letter ‘H’, as seen in a 8x8 configuration, (a) under no turbulence, and (b) under moderate turbulence. 

    When detected with an array of photo-detectors, the image of ‘H’ looks blurred under turbulence, with overlap of energy among the pixels (Figure 4b). The blurred image can be corrected by different blind deconvolution algorithms. The post-processed result of one algorithm, namely Approximate Factorization of Bivariate Polynomials, is shown in Figure 5c.

   

    Figure 5. Letter ‘H’ detected by 8x8 array of photo-detectors, (a) under no turbulence, and (b) under moderate turbulence, (c) after blind deconvolution by AFBP algorithm.

    The visual clarity can be further improved by applying adaptive optics (AO) correction to the image before post-processing, which corrects for the optical aberrations. Table 2 below summarizes the % MSE and SNR Improvement factors with and without the use of adaptive optics and blind deconvolution. Clearly, a combination of these techniques leads to a more practical design.

Table 2:  BD performance improvement with AO correction, using  ordered Zernike Polynomials Modal Expansion.

Zernike Polynomials and Modal Expansion

 

On the receiver side, an N×N array of photo-detectors is used to receive the reflections from the target.

Receiver Design

Figure 6 Receiver design using Holographic Optical Elements (HOE) and APD Array

Table 3  Receiver Design Parameters: IC = Ideal Optical Concentrator and Filter is an Interference Filter

    Successful implementation of these techniques will transform military surveillance applications, and open the door to an all-weather imaging solution with lower probability of false alarm.

  1. G. Yun, M. Kavehrad, "Spot-Diffusing and Fly-Eye Receivers for Indoor Infrared Radio Communications," IEEE Int. Conf. on Selected Topics in Wireless Communications, Vancouver, June 1992.

  2. Joseph Kahn, et al., “Imaging Diversity Receivers for high-Speed Infrared Wireless Communication,” IEEE Communications Magazine, Vol. 36, No. 12, pp. 88-94, December 1998.

  3. M. Kavehrad, Z. Hajjarian, J. Fadlullah, "Combating Scintillation and Dispersion on a Laser Imaging Link using Multiple Parallel Beams," OSA Topical Meeting, San Diego, CA, February 2010.

  4. Z. Hajjarian, M. Kavehrad and J. Fadlullah, ”Analysis of  Wireless Optical Communications Feasibility in Presence of Clouds Using Markov Chains,” IEEE Journal on Selected Areas in Communications, Vol. 27, No. 9, Decemebr 2009.

  5. Z. Hajjarian, J. Fadlullah and M. Kavehrad, "MIMO Free Space Optical Communications in Turbid and Turbulent Atmosphere," Invited Paper, Journal of Communications, Vol.  4, No. 8, 524-532, September 2009.

  6. M. Kavehrad, Z. Hajjarian, J. Fadullah, "Spatially Multiplexed Optical MIMO Imaging System in Cloudy Turbulent Atmosphere," Proceedings of the SPIE Optics+Photonics Conference, San Diego, California, August 2009.

  7. Z. Hajjarian, M. Kavehrad, "Using MIMO Transmissions in Free Space Optical Communications in Presence of Clouds and Turbulence," Proceedings of the SPIE Photonics West, San Jose, California, Jan. 2009.

  8. Z. Hajjarian, Jarir Fadlullah, M. Kavehrad, "Use of Markov Chain in Atmospheric Channel Modeling of Free Space Laser Communications," Proceedings of the IEEE MILCOM, San Diego, CA., November 2008.

  9. Z. Hajjarian and M. Kavehrad, “Channel Modeling in Wireless Optical Communications using Markov Chains,” Proceedings of IEEE CCECE, Niagara Falls, Ontario, Canada, May 2008.

  10. S. Jivkova, M. Kavehrad, "Indoor Wireless Infrared Local Access, Multi-Spot Diffusing with Computer Generated Holographic Beam-Splitter," Proceedings of ICC'99, Vancouver, CANADA, June 1999.

  11. M. Kavehrad, "Mitigation Approaches for Optical Imaging Through Clouds and Fog,” DARPA/AFRL Final Report: AFRL-RY-WP-TR-2009-1331, Released on December 9, 2009.

            News Items:

Free-space optical communications for terrestrial and space-borne applications are alive and well thanks to steady advances

 in light sources and detection schemes that extend data rates and physical reach despite atmospheric challenges.

GAIL OVERTON, senior editor

Laser Focus

 

PDF COPY

 ACKNOWLEDGEMENTS

A DARPA Grant sponsored by the U.S. Air Force Research Laboratory/Wright-Patterson AFB Contract-FA8650-08-C-7850 and Pennsylvania State University CICTR have supported this research.

The final report was cleared through public release on 7 Dec 2009.  PA number is 88 ABW-09-5069.  Likewise the final report is in DTIC as an approved for public release document.

__________________________________________________________-

Return to top of page

 

ENGEDWORKS
icons representing the world, learning, discovery, and engagement